Extended Kalman Filter in Orekit

Posted on 2019-04-23 Edited on 2019-05-03 In Techniques , Software Views: Disqus:

Covariance/noise matrix 在 body frame 和 inertial frame 之间的转换

这部分代码出现在 UnivariateProcessNoise 中，see
#537: `FIXME` in codes
#403: Add a provider generating process noise increasing in time, for better Kalman filtering
for more discussions.

RSW === LVLH in Orekit.

lofCartesianProcessNoiseMatrix Local orbital frame (RSW, or LVLH) 中的 covariance $Q^{RSW}$

GP-prediction covariance, a diagonal 6 x 6 matrix. (in my codes)

jacLofToInertial $J_{R2I} = J_{RSW\rightarrow Iner.} = \frac{\partial X^{Iner.}}{\partial X^{RSW}}$

Question? Is there a loss of information at this step?

jacParametersWrtCartesian $J_{P2C} = J_{Par.\rightarrow Cart.} = \frac{\partial Par.}{\partial Cart.} = \frac{\partial Par.}{\partial X^{Iner.}}$

If the parameters used to represent the orbit is inertial Cartesian, then this should be $I_6$ .
Otherwise, it’s not.

Finial conversion:

\begin{aligned} Q^{Iner.} &= Q^{Par.} \\ &= \frac{\partial Par.}{\partial X^{Iner.}} \frac{\partial X^{Iner.}}{\partial X^{RSW}} Q^{RSW} \left(\frac{\partial X^{Iner.}}{\partial X^{RSW}}\right)^T \left(\frac{\partial Par.}{\partial X^{Iner.}}\right)^T \\ &= J_{P2C} \cdot J_{R2I} \cdot Q^{RSW} J_{R2I}^T \cdot J_{P2C}^T \end{aligned}

inverse: from Inertial to RSW

Simple:

J_{R2I}^{-1} \cdot J_{P2C}^{-1} \cdot Q^{Iner.} \cdot J_{P2C}^{-T} \cdot J_{R2I}^{-T} = Q^{RSW}

代码细节

总结：

在 Hipparchus 中，需要估计的动力学模型被称为 process (NonLinearProcess)；在 Orekit 中，Model即是这个 process。
在 Hipparchus 中， estimator 计算过程中的结果称为 ProcessEstimate， process 的计算结果称为 evolution (NonLinearEvolution.java)；在 Orekit 中，estimator 的计算结果称为 ~~KalmanEstimation~~ (被我修改为 KalmanEstimate ，其它地方全是这么叫的，用 estimation 混乱。) [TODO: feed back to Orekit]
Hipparchus 只处理 normalized values， Orekit 通过 Model 来实现 dimensional value 和 normalized value 之前的交互。
Hipparchus 只需要调用 Model 中的 getEvolution() 和 getInnovation()； Model 中的所有其它内容，全部是处理 dynamics, normalizing/unnormalizing…
想要的 EKF 的结果直接从 Orekit 的 KalmanEstimator 中找相应函数，基本都是 Model 中对应函数的 wrapper。新功能在通过修改 KalmanEstimator 来实现好过修改 Model （因为后者是 package private 的包，将来可能有很大的改动）。

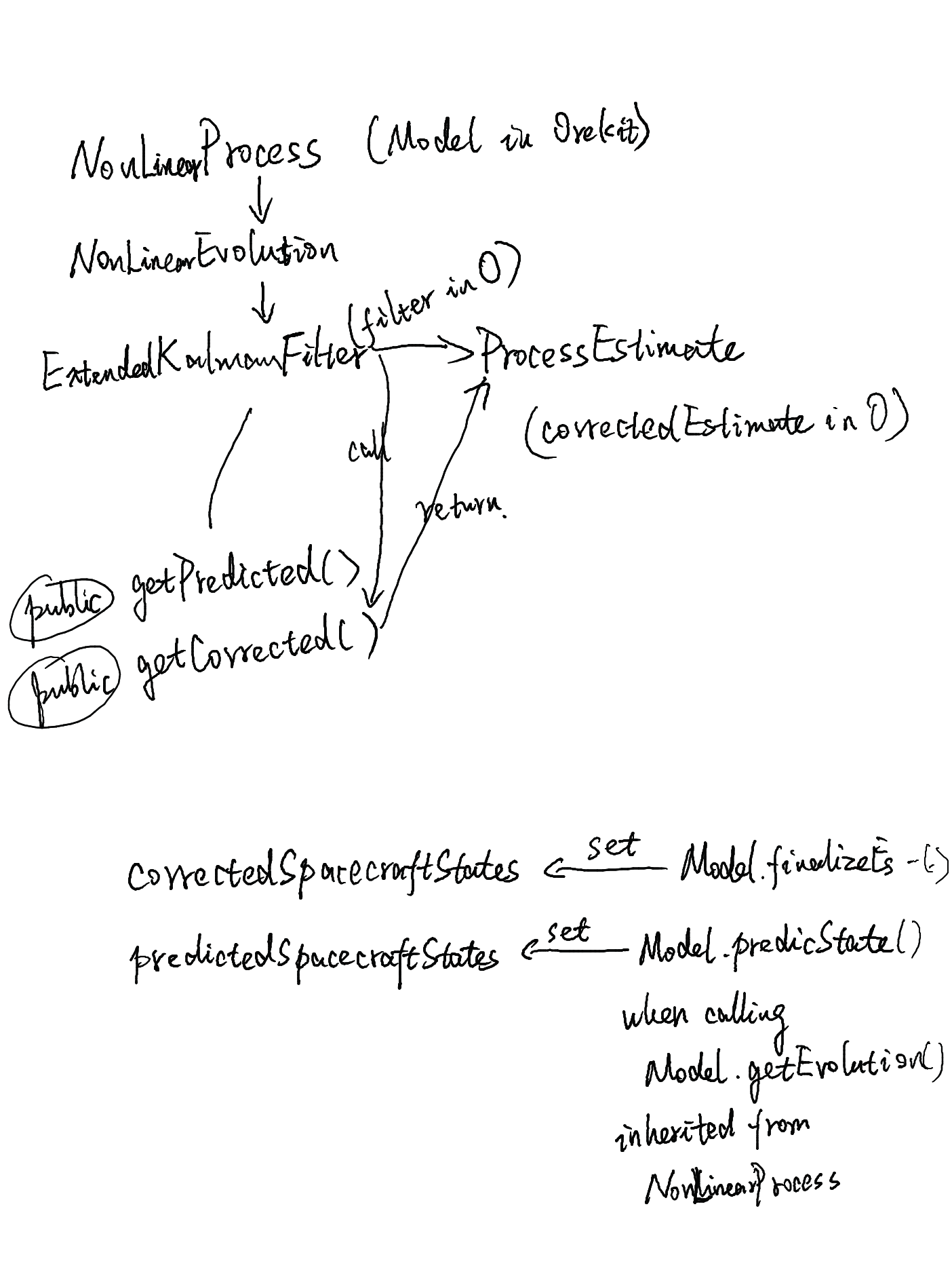
Where each values are stored

ExtendedKalmanFilter 实现了 AbstractKalmanFilter 实现了 KalmanFilter （单步更新，然后读取预测和更新的结果）。

Orekit.*.Model 实现了 Hipparchus.*.NonLinearProcess。计算结果存在为 Hipparchus.*.NonLinearEvolution。

Orekit.*.KalmanEstimator.estimateStep 中调用 filter.estimationStep() 返回的是 Hipparchus.*.ProcessEstimate ，包含了 $k$ , $X_{k|k}$ , $P_{k|k}$ , $STM_{k|k-1}$ , $H_k$ , $S_k$ , $K_k$ 。

Process noise

UnivariateProcessNoise 接受输入为：
初始误差initialCovarianceMatrix，
RSW系轨道参数噪声函数lofCartesianOrbitalParametersEvolution，
模型过程噪声函数propagationParametersEvolution。

Get predicted covariance (with/without noise) at every epochs without duplicate propagation

AbstractKalmanFilter.java 中的 correct() 中可以利用下面这段代码，跳过当前 measurement 导致的更新过程，可以实现连续预测，在每个 epoch 得到相应的 predictedState, predictedCovariance, noise

if (innovation == null) {
    // measurement should be ignored
    corrected = predicted;
    return;
}

Problems !

The covariance input used to construct PV measurement is not kept by the constructor!!! It is replaced by extracting sigma, i.e. square root of the diagonal of the covariance. Orekit should mention this at some place (TODO: check and feedback). 之前理解错误，是保留了covariance的，在AbstractMeasurement中只保存sigma，但是PV保存了covariance。

General Orekit

Hybrid Kalman Filter

和这个概念更接近，参见 Wikipedia: Kalman_filter#Hybrid_Kalman_filter。

Discrete-time measurements

或者是这个概念，参见 Wikipedia: Discrete-time_measurements。

Porpagator/Propagation paramerters 即是模型参数

See this Orekit architecture description:

one list containing the 6 orbital parameters, which are estimated by default

one list containing the propagator parameters, which depends on the force models used and are not estimated by default

one list containing the measurements parameters, which are not estimated by default

对 process noise 的实现

积分state时使用 $\dot\bm{x} = f(\bm{x})$ ，没有process noise。
积分state transition matrix时使用 $\partial f/\partial \bm{x}$ ，同样没有process noise。
最后计算covariance时需要添加process noise $Q$ ，可以假设是依赖于时间的 $Q(t)$ 。

General EKF

Equations

from Wikipedia: Discrete-time predict and update equations

Prediction:

Predicted state estimate
$\hat{\bm{x}}_{k|k-1} = f(\hat{\bm{x}}_{k-1|k-1},\bm{u}_k)$
Predicted covariance estimate
$\bm{P}_{k|k-1} = \bm{F}_k \bm{P}_{k-1|k-1} \bm{F}_k^\top+\bm{Q}_k$

Update:

Innovation or measurement residual
$\tilde{\bm{y}}_k = \bm{z}_k - h(\hat{\bm{x}}_{k|k-1})$
Innovation (or residual) covariance
$\bm{S}_k = \bm{H}_k \bm{P}_{k|k-1} \bm{H}_k^\top + \bm{R}_k$
Near-optimal Kalman gain
$\bm{K}_k = \bm{P}_{k|k-1} \bm{H}_k^\top \bm{S}_k^{-1}$
Updated state estimate
$\hat{\bm{x}}_{k|k} = \hat{\bm{x}}_{k|k-1} + \bm{K}_k \tilde{\bm{y}}_k$
Updated covariance estimate
$\bm{P}_{k|k} = (\bm{I} - \bm{K}_k \bm{H}_k) \bm{P}_{k|k-1}$

实际上更应该使用 Continuous-time extended Kalman filter with discrete-time measurements，公式都差不多。

In my study,

如果 $h(\xi)=\xi$ ， $H_k = I_6$ ,
则
$S_k=P_{k|k-1}+R_k$
$K_k=P_{k|k-1}S_k^{-1}=\frac{P_{k|k-1}}{P_{k|k-1}+R_k}$
则
$\hat{\bm{x}}_{k|k}=\hat{\bm{x}}_{k|k-1}+K_k\tilde{\bm{y}}_k = \frac{R_k}{P_{k|k-1}+R_k}\hat{\bm{x}}_{k|k-1} + \frac{P_{k|k-1}}{P_{k|k-1}+R_k} \bm{z}$
$P_{k|k}=(I-K_k)P_{k|k-1} = \frac{R_k}{P_{k|k-1}+R_k}\cdot P_{k|k-1} = \frac{P_{k|k-1}}{P_{k|k-1}+R_k}\cdot R_k$
是否
$P_{k|k} = K_k\cdot R_k$ ？

问题：
$P_{k|k}$ 总是要“小于” 预测的不确定性 $P_{k|k-1}$ 和观测误差 $R_k$ ？
当 $P_{k|k-1}$ 和 $R_k$ 其中之一远大于另一个时， $P_{k|k}$ 完成退化为较小的一个。

Testing results:

force $P_{k|k} = P_{k|k-1}$ : test the conversion from inertial to RSW; covariance should be identical to EKF pure. [checked, correct.]
force $P_{k|k} = R_k$ : test the conversion from RSW to inertial; covariance should be identical to GP pure. [checked, correct.]
force $P_{k|k-1}$ equals $R_k$ : test the updating process; covariance should be half of them while standard deviation should be $1/\sqrt{2}$ of them. [checked, correct.]

So, all calculations are correct.